Ragam Teknik Analisis Data & Uji Hipotesis Asosiatif

Teknik analisis data sangat berperan dalam menjawab tujuan penelitian dan pendugaan hipotesis. Hipotesis dibutuhkan untuk membuktikan kebenaran yang ada di lapangan serta menguji fenomena yang terjadi. Salah satu penggunaan hipotesis yang umum dipakai oleh peneliti adalah hipotesis asosiatif. Hipotesis asosiatif masuk ke dalam tiga jenis hipotesis dalam metode penelitian.

Berdasarkan definisinya, hipotesis asosiatif berarti jawaban sementara terhadap suatu hubungan berupa asosiatif antara dua variabel atau lebih. Hipotesis asosiatif juga kerap dikenal dalam penelitian korelasional atau penelitian yang menguji apakah variabel tersebut memiliki korelasi (hubungan) terhadap variabel lain dalam suatu populasi.

Hipotesis asosiatif adalah bentuk pernyataan yang menunjukkan bahwa variabel yang diuji terjadi bersama-sama dalam beberapa cara tertentu tanpa menyiratkan bahwa yang satu memiliki sebab yang lain. Pada kesamaannya hipotesis asosiatif dapat diterapkan dalam berbagai jenis data.

Mulai dari data ordinal, nominal, rasio dan interval. Untuk melakukan hipotesis asosiatif ini dibutuhkan teknik analisis data yang tepat agar bisa menjawab tujuan penelitian dan dugaan yang kita ajukan sebelumnya. 

Hal ini dikarenakan hipotesis asosiatif perlu dilakukan pengujian berupa teknik analisis data yaitu pengujian hipotesis asosiatif dengan menggunakan beberapa uji. Bagi sahabat DQLab yang penasaran dengan hipotesis asosiatif dan apa saja uji-ujinya, kali ini DQLab akan bahas lebih lanjut dalam artikel ini. 

1. Pengertian Hipotesis Asosiatif

Sebelum kita bahas terkait pengujian hipotesis asosiatif, kita samakan pemahaman dulu ya sahabat DQLab terkait pengertian dari hipotesis asosiatif. Gulo (2000), hipotesis asosiatif biasanya berada pada variabel yang memiliki kesamaan jenis data, berupa ordinal, interval, ataupun rasio.

Terkadang salah satu variabel juga ada yang interval, ada yang rasio, ada juga yang nominal dan lain-lain. Jadi, hubungan asosiatif memberikan penekanan bahwa kedua variabel sama-sama berubah. Berubah disini bisa karena adanya hubungan positif ataupun negatif terhadap antar variabel yang diuji.

Menurut Zulfikar (2014), membagi hipotesis asosiatif menjadi tiga bagian diantaranya:

• Hipotesis hubungan simetris yaitu hubungan yang lebih menekankan hubungan kebersamaan antara variabel, bukan hubungan sebab akibat. Contoh: adanya hubungan antara luas lahan dengan produksi komoditas, hubungan antara nilai tukar dengan daya saing ekspor, hubungan antara usia konsumen dengan perilaku pelanggan.

  
  

• Hipotesis hubungan sebab akibat yaitu hubungan yang sifatnya saling mempengaruhi dengan kata lain, mempengaruhi secara sebab akibat antara dua variabel atau lebih. Contoh: GDP Amerika Serikat dan nilai tukar berpengaruh positif dan signifikan terhadap ekspor alas kaki Indonesia ke Amerika Serikat, harga berpengaruh positif dan tidak signifikan terhadap ekspor alas kaki Indonesia ke Amerika Serikat, dan produksi berpengaruh negatif dan tidak signifikan terhadap ekspor alas kaki Indonesia ke Amerika Serikat.

  
  

• Hipotesis interaktif, jenis hipotesis asosiatif ini merupakan hubungan antara variabel yang saling mempengaruhi. Bila hipotesis interaktif adalah hubungan timbal balik. Contoh: terdapat hubungan yang saling mempengaruhi antara tingkat infiltrasi dengan permeabilitas tanah, terdapat hubungan yang saling mempengaruhi antara curah hujan dengan evaporasi, terdapat hubungan yang saling mempengaruhi antara laju sedimen dengan tingkat erosi, terdapat hubungan yang saling mempengaruhi antara pencemaran sungai dengan limbah masyarakat.

Baca juga: Teknik Analisis Data CRISP-DM dalam Data Mining

2. Uji Hipotesis Asosiatif: Spearman Rank

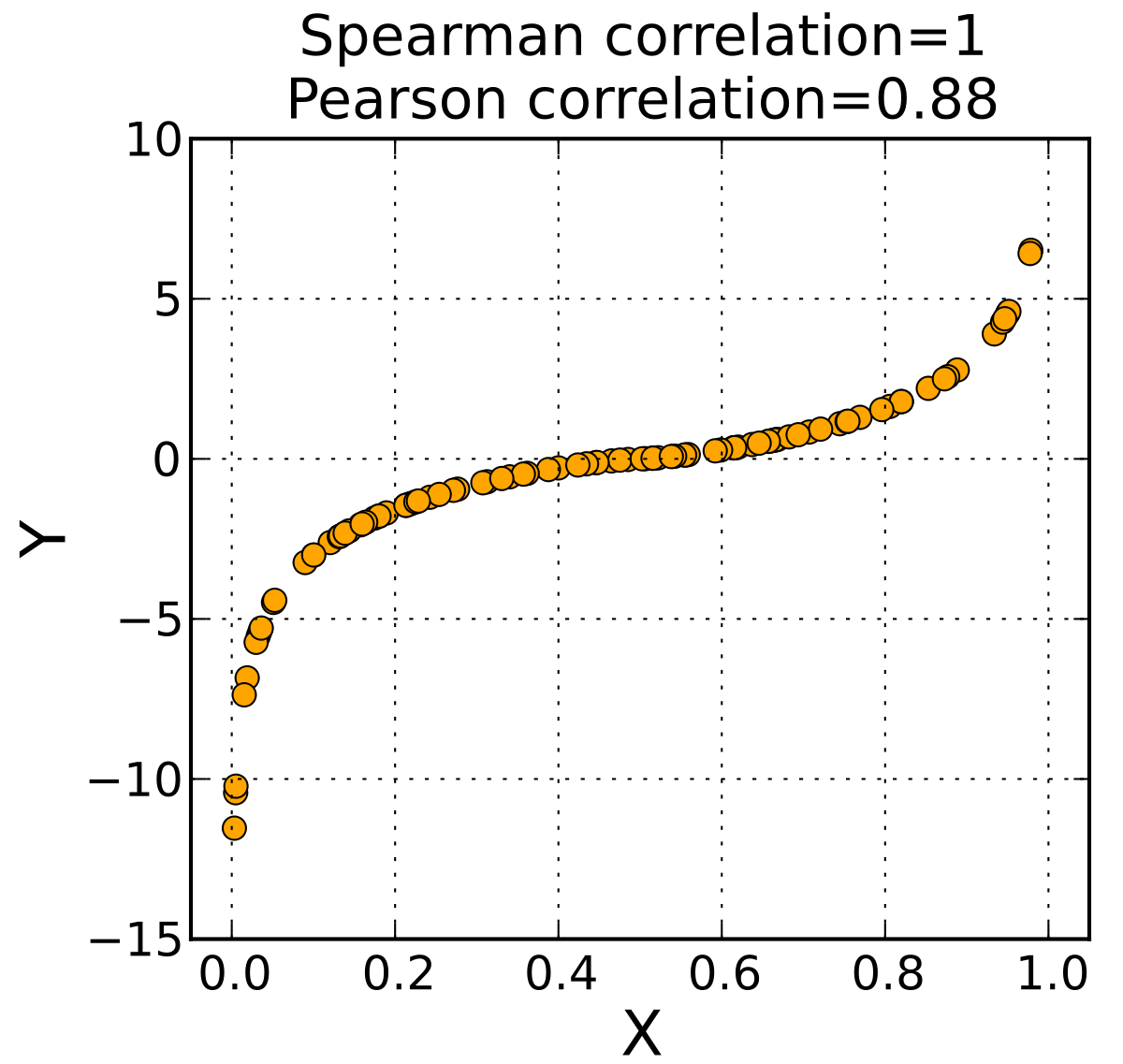
Korelasi Rank Spearman atau yang biasanya disebut dengan Spearman Rank Correlation Coefficient merupakan salah satu penerapan koefisien korelasi dalam metode analisis data statistik non parametrik.

Statistik non parametrik ini merupakan suatu ukuran asosiasi atau hubungan yang dapat digunakan pada kondisi satu atau kedua variabel yang diukur adalah skala ordinal (berbentuk ranking) atau kedua variabel adalah kuantitatif namun kondisi normal tidak terpenuhi.

Statistik nonparametrik mengasumsikan statistik yang digunakan ketika data tidak memiliki informasi parameter, data tidak berdistribusi normal atau data diukur dalam bentuk ranking. Pembuatan ranking dapat dimulai dari nilai terkecil atau nilai terbesar tergantung permasalahannya. 

Bila ada data yang nilainya sama, maka pembuatan ranking didasarkan pada nilai rata-rata dari ranking-ranking data tersebut. Apabila proporsi angka yang sama tidak besar, maka formula diatas masih bisa digunakan. Namun apabila proporsi angka yang sama cukup besar, maka dapat digunakan suatu faktor koreksi.

Simbol ukuran populasinya adalah Ï dan ukuran sampelnya rs. Berbeda dengan Korelasi Pearson, korelasi ini tidak memerlukan asumsi normalitas, maka korelasi rank spearman cocok juga digunakan untuk data dengan sampel kecil.

Kekuatan dari korelasi juga ikut menentukan signifikansi hubungan dari dua variabel yang dilakukan uji ini. Ketika nilai sig (2 tailed) berada kurang dari rentan 0,05 atau 0,01, maka hubungan dikatakan signifikan. Sedangkan pada saat nilai sig (2 tailed) berada lebih dari rentang tersebut maka hubungan dikatakan tidak berarti.

Arah korelasi dapat dilihat di hasil bagaimana angka koefisien korelasi dan biasanya nilai yang dihasilkan berada pada rentang -1 sampai dengan 1. Ketika nilai koefisien korelasi memiliki nilai negatif maka hubungan tidak searah sedangkan ketika bernilai positif maka hubungan searah.

3. Uji Hipotesis Asosiatif: Kendall Tau

Korelasi Kendall Tau merupakan statistik nonparametrik yang dipakai untuk menguji hipotesis asosiatif. 

Beberapa syarat yang harus dipenuhi untuk melakukan pengujian korelasi Kendall Tau adalah

• Skala data ordinal ataupun kontinu. Data ordinal adalah data yang berupa kategorik, namun memiliki tingkatan, sehingga bisa kita beri ranking dengan mudah. Misalnya klasifikasi tingkat pendidikan SD – SMP – SMA – Perguruan Tinggi merupakan salah satu bentuk data ordinal. Sedangkan data kontinu adalah data numerik. Contohnya seperti nilai ujian matematika, gaji, berat badan, dan lainnya.

  
  

• Dua variabel memiliki hubungan monotonic. Dalam artian, kenaikan nilai variabel pertama juga akan disertai dengan kenaikan atau penurunan nilai variabel kedua. Contoh hubungan monotonic seperti hubungan antara nilai ujian matematika dan fisika.

  Sementara hubungan non-monotonic bisa kita jumpai pada hubungan antara usia pemain sepak bola dengan performanya di lapangan. Di mana performa pemain semakin meningkat ketika usia mendekati 30, namun mengalami penurunan saat usia sudah melewati angka 30 tahun.

Baca juga : Langkah-Langkah Menggunakan Teknik Analisis Data Kualitatif

4. Uji Hipotesis Asosiatif: Pearson Product Moment

Uji hipotesis asosiatif selanjutnya adalah Pearson Correlation Product Moment. Uji Pearson Correlation Product Moment adalah salah satu parametrik dari beberapa jenis uji korelasi yang digunakan untuk mengetahui derajat keeratan hubungan 2 variabel yang memiliki jenis interval atau rasio dan memiliki distribusi data yang normal, dimana dengan uji ini akan menghasilkan nilai koefisien korelasi yang nilainya berkisar antara -1, 0 dan 1. 

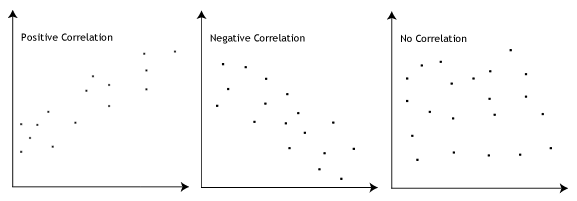
Nilai -1 artinya terdapat korelasi negatif yang sempurna, 0 artinya tidak ada korelasi dan nilai 1 berarti ada korelasi positif yang sempurna.

Ingin berkarir di bidang data science tapi, tidak memiliki background pendidikan yang linier dengan itu? Mengingat skill data science terbilang cukup banyak yang wajib dikuasai salah satunya adalah memahami algoritma data science nya hingga tahap penerapannya pada dataset. 

Yuk, coba free module Introduction to Data Science with R dan python dari DQLab sekarang. Caranya gimana? Mudah banget kok cukup signup sekarang ke DQLab.id lalu pilih menu learn.

Setelah itu kamu sudah bisa menikmati pembelajaran yang praktis dan aplikatif dan jago algoritma data science bersama DQLab! Tunggu apa lagi? Yuk, signup sekarang dan mulai belajar Module Premium di DQLab!

Penulis: Reyvan Maulid