Digital Transformation: Yuk Pelajari Ukuran dalam Ilmu Statistik Sebelum Melakukan Pengolahan Data!
Salah satu ilmu penting di era digital transformation adalah ilmu statistika. Statistika merupakan ilmu yang mempelajari cara pengumpulan data, pengolahan data, analisis data, dan penyajian hasil analisis yang dapat digunakan untuk pengambilan keputusan. Ilmu statistika dibagi menjadi dua yaitu statistik deskriptif dan statistik inferensial. Statistik deskriptif adalah metode dan prosedur yang digunakan untuk pengumpulan, pengorganisasian, presentasi dan memberikan karakteristik terhadap himpunan data. Statistik inferensial adalah prosedur yang digunakan untuk mengambil suatu inferensi (kesimpulan) tentang karakteristik populasi atas dasar informasi yang dikandung dalam sebuah sampel.
Statistika selalu berhubungan dengan data. Data yang belum pernah diproses sama sekali disebut dengan data mentah atau raw data. Umumnya data mentah yang dihasilkan dari sumber yang berbeda tidak lengkap, tidak konsisten, dan rawan kesalahan. Pengolahan awal pada sebuah data merupakan langkah penting dalam machine learning. Pengolahan ini biasa disebut dengan preprocessing data. Preprocessing data membantu machine learning untuk belajar dan bekerja lebih baik dengan menyediakan data yang bersih dari sekumpulan data mentah. Ada banyak teknik preprocessing yang dapat digunakan. Namun, kita harus memahami sifat data sebelum menggunakan teknik preprocessing. Untuk memahami sifat suatu kumpulan data, kita harus memahami ukuran statistik. Nah, kali ini, DQLab akan menjelaskan apa saja ukuran statistik yang harus dipahami sebelum melakukan preprocessing. Jadi, baca artikelnya sampai selesai ya!
1. Ukuran Tendensi Pusat
Ukuran tendensi pusat merupakan nilai tunggal yang menggambarkan sekumpulan data dengan mengidentifikasi nilai pusat dalam kumpulan data tersebut. Ukuran tendensi pusat dibagi menjadi tiga ukuran yaitu ukuran distributif, aljabar dan holistik. Ukuran distributif digunakan untuk kumpulan data tertentu dengan membagi data menjadi subset yang lebih kecil, menghitung ukuran untuk setiap subset dan kemudian menggabungkan hasilnya sebagai nilai pengukuran untuk seluruh data. Contohnya, penjumlahan dapat dihitung untuk setiap subset data yang lebih kecil kemudian digabungkan untuk mendapatkan penjumlahan akhir dari keseluruhan data. Contoh lain dari ukuran distributif adalah menghitung nilai maksimal dan nilai minimal. Ukuran aljabar merupakan ukuran yang menerapkan fungsi aljabar ke satu atau lebih ukuran distributif. Ukuran aljabar yang paling umum dan paling populer adalah mean (rata-rata). Rumus mean adalah
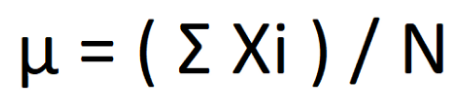
Sigma Xi adalah jumlah keseluruhan data dan N adalah banyaknya data. Beberapa nilai dalam himpunan dapat dikaitkan dengan bobot. Bobot mencerminkan signifikansi, kepentingan, atau frekuensi kejadian yang disisipkan pada masing-masing data. Dalam kasus ini, mean yang digunakan adalah weighted mean atau rata-rata tertimbang. Rumus weighted mean didefinisikan sebagai berikut
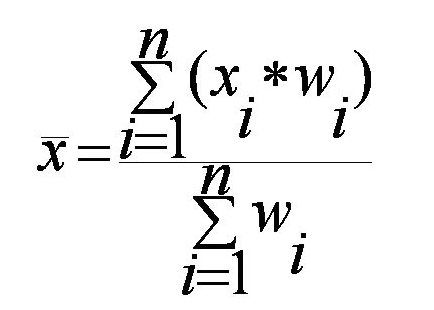
Ukuran holistik merupakan ukuran yang dapat dihitung pada seluruh kumpulan data secara keseluruhan. Ukuran ini tidak dapat dihitung dengan membagi data menjadi subset dan menggabungkan nilai yang diperoleh sebagai nilai keseluruhan data. Ukuran holistik paling populer yang digunakan untuk memahami ukuran tendensi pusat dari data adalah median dan modus.
Baca Juga: Teknik Pengolahan Data: Yuk Pelajari Teknik Pengolahan Data yang Tepat Sesuai Tujuan Penelitianmu!
2. Fungsi Ukuran Tendensi Pusat
Setelah mempelajari metode untuk menghitung ukuran tendensi pusat, sekarang kita akan belajar alasan mengapa kita harus memahami metode tersebut. Fungsi ukuran tendensi pusat adalah untuk melihat kecenderungan data (skewness) dan melihat adanya missing value pada kumpulan data.
Skewness adalah asimetri dalam distribusi data pada statistik. ada dua jenis skewness yaitu positive skewness dan negative skewness. Suatu grafik distribusi dikatakan memiliki positive skewness apabila frekuensi data bernilai rendah lebih banyak dan mendominasi seluruh kumpulan data. pada keadaan ini nilai modus
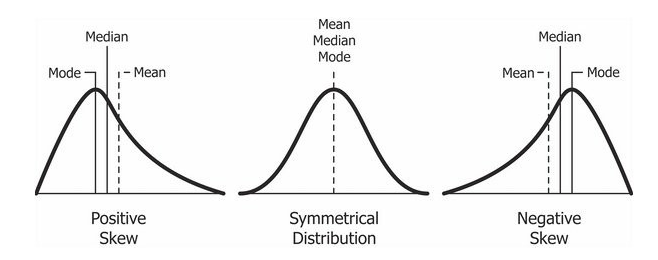
Alasan kedua mengapa kita harus memahami metode ukuran tendensi pusat adalah untuk mengidentifikasi adanya missing value. Kumpulan data mentah bisa saja berisi banyak kesalahan dan missing value yang dapat mengubah model sehingga hasil analisis tidak sesuai. Untuk mengatasi masalah ini, nilai-nilai yang mewakili tendensi pusat dari kumpulan data umumnya digunakan untuk mengisi nilai-nilai yang hilang karena nilai-nilai tersebut diasumsikan untuk memberikan gambaran mengenai sifat data.
3. Ukuran Penyebaran Data
Ukuran sebaran data merupakan metode untuk mendeskripsikan besarnya sebaran data. Ukuran paling populer untuk mengukur penyebaran data adalah range, kuartil, interkuartil dan simpangan baku atau standar deviasi. Range merupakan perbedaan antara nilai terbesar atau nilai maksimum dan nilai terkecil atau terendah dari kumpulan data. Kuartil adalah persentil ke-k dari kumpulan data Ada tiga kuartil berbeda untuk tiga nilai k yaitu kuartil Pertama (k = 25), median (k=50), dan kuartil ketiga (k=75). Kuartil pertama adalah titik yang mencakup 25% data kebawah pada kumpulan data. Median atau kuartil kedua adalah nilai tengah kumpulan data dan 50% dari sekumpulan data berada pada rentang ini. Kuartil Ketiga adalah titik yang mencakup 75% keatas dari keseluruhan data. Interquartile atau biasa dikenal dengan interquartile range (IQR) merupakan Selisih antara kuartil ketiga (Q3) dan kuartil pertama (Q1). Standar deviasi merupakan metode untuk mengukur sebaran data di sekitar rata-rata suatu data. Jika sebaran data semakin lebar, maka nilai standar deviasi semakin kecil, begitu pula sebaliknya. Standar deviasi didefinisikan sebagai berikut
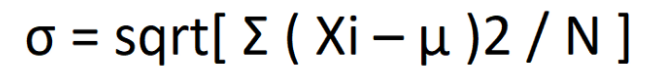
Pengolahan data pada ilmu statistika merupakan salah satu langkah penting dalam ilmu data science. Keahlian statistik dan ilmu data science merupakan kombinasi yang "mahal" dan banyak dibutuhkan. Data science saat ini merupakan ilmu yang paling banyak dicari karena dapat digunakan di berbagai aspek dan industri. Oleh karena itu, belajar data science sama pentingnya dengan belajar statistik.
4. Yuk, Mulai Belajar Data Science bersama DQLab secara GRATIS!
Tidak memiliki background IT? Jangan khawatir, kamu tetap bisa menguasai Ilmu Data Science untuk siap berkarir di revolusi industri 4.0. Bangun proyek dan portofolio datamu bersama DQLab untuk mulai berkarir di industi! Sign up sekarang untuk #MulaiBelajarData di DQLab!
Simak informasi di bawah ini untuk mengakses gratis module "Introduction to Data Science":
Buat Akun Gratis dengan Signup di DQLab.id/signup
Akses module Introduction to Data Science
Selesaikan modulenya, dapatkan sertifikat & reward menarik dari DQLab
Subscribe DQLab.id untuk Akses Semua Module Premium!
Penulis: Galuh Nurvinda Kurniawati
Editor: Annissa Widya Davita

