Kenalan dengan Model Regresi Linear Bahasa R dan Aplikasinya

Siapa yang tidak kenal dengan model regresi linear? Salah satu metode analisis data yang sering digunakan dalam penelitian. Walaupun analisis ini terbilang klasik bagi jurusan yang berbau statistik, namun model regresi linear sangatlah umum digunakan untuk analisis data pada topik-topik program studi lain.
Meskipun penggunaan modelnya sederhana dan mudah untuk diikuti pemula, analisis regresi memiliki banyak manfaat untuk menjawab tujuan penelitian. Idealnya regresi menganalisis tentang pengaruh dari variabel independen terhadap variabel dependen.
Secara umum, model regresi linear dibagi menjadi dua jenis. Pertama model regresi linear sederhana yang melibatkan antara satu variabel dependen dengan satu variabel independen. Sedangkan jenis kedua yaitu regresi linear berganda yang melibatkan satu variabel dependen terhadap lebih dari satu variabel dependen.
Banyak software yang bisa kamu manfaatkan nih sahabat DQLab untuk melakukan analisis regresi. Salah satunya kita bisa aplikasikan dengan menggunakan bahasa R. Kira-kira bagaimana ya implementasi dari penggunaan analisis regresi dengan bahasa R.
Yuk kita kulik bersama melalui module baru DQLab œR Language, Data Preparation & Exploratory Data Analysis [EDA] - Mengenal Model Regresi Linear & R. Pada module ini kamu akan mendapatkan beberapa pemahaman skill baru diantaranya adalah :
Mengerti apa dan kenapa Regresi dan Regresi Linear
Mengenal konsep Least Squares Fit dan pemanfaatannya dalam Regresi Linear
Mampu mengerti dataset penjualan permen, sereal, dan pisang serta tingkat kerusakan gigi
Mampu membaca dan menggabungkan dua file tsv yang digunakan sebagai dataset
Mampu melakukan proses Regresi Linear pada R dengan metode fit dari LinearRegression dan membuat data model tingkat kerusakan gigi dan hubungannya dengan penjualan permen, dan bukannya penjualan item lain
(Catatan: karena delayed effect dari makanan terhadap gigi, maka data seri tingkat kerusakan gigi perlu digeser 4 bulan, ini hanya perkiraan fiktif karena langsung makan permen tentu tidak langsung merusak gigi. Misalkan beli mulai Januari dan makan terus, maka efeknya akan terlihat di April atau Mei. Silahkan berkreasi bagaimana temuan pergeseran 4 bulan ini menjadi hal menarik seperti œeureka moment di cerita ini)Mampu menggunakan metode predict untuk melakukan prediksi nilai data dari model yang dihasilkan (tingkat kunjungan dokter gigi dengan input jumlah penjualan permen)
Setelah kita tahu learning outcomes pada modul ini, mari kita belajar bareng bersama yuk sahabat DQLab.
1. Apa itu Model Regresi Linear?
Regresi merupakan suatu model dalam statistik yang berfungsi untuk mencari hubungan antara variabel bebas atau yang sering disebut dengan variabel independen atau prediktor dengan variabel dependen atau sering disebut dengan respon. Secara umum, bentuk persamaan dari model regresi dapat dirumuskan sebagai berikut:
y = f(x)
Dimana nilai y merupakan nilai dari respons yang bergantung pada sebuah fungsi dari variabel x (f(x)). Secara umum f(x) ini dapat terdiri dari:
Fungsi linear
Fungsi Kuadratik
Fungsi Log
Fungsi Eksponensial, dan sebagainya.
Dalam pembahasan kali ini, kita akan fokus belajar menggunakan fungsi linear dengan satu buah variabel bebas yang sering disebut dengan regresi linear. Regresi linear dapat digunakan ketika terdapat hubungan yang linear antara variabel independen dan variabel dependen. Berikut ini adalah bentuk persamaan umum sebuah model regresi dengan menggunakan fungsi linear:
y = a + bx
Dimana y merupakan nilai prediksi, a merupakan sebuah variabel intercept. Intercept merupakan titik dimana garis regresi akan memotong sumbu y ketika x bernilai sama dengan 0.
Dengan kata lain, intercept adalah nilai perubahan variabel y ketika x bernilai 0. Variabel b, b merupakan konstanta untuk menunjukkan besar perubahan variabel y untuk setiap kenaikan 1 variabel x dan e merupakan nilai error. Nilai dari a, b ini dapat teman-teman hitung dengan menggunakan metode kuadrat terkecil atau yang sering disebut dengan least-square method.
Baca Juga: Kursus Belajar Data dengan Bahasa R Untuk Pemula
2. Apa itu Metode Least Square
Seperti yang sudah dijelaskan sebelumnya bahwa salah satu penggunaan regresi linear didekatkan dengan penggunaan metode least square. Dalam suatu penelitian tertentu, metode Least Square merupakan salah satu metode berupa data deret berkala atau time series.
Metode ini dibutuhkan data dimasa lampau untuk melakukan peramalan penjualan dimasa mendatang sehingga dapat ditentukan hasilnya. Least Square adalah metode peramalan yang digunakan untuk melihat trend dari data deret waktu.
Metode least square method adalah metode yang digunakan untuk menentukan nilai dari koefisien dalam model regresi. Pada dasarnya metode least square adalah mencari model regresi terbaik yang memiliki nilai error yang terkecil.
Misalkan dalam sebuah dataset kita memiliki pasangan data yixi dimana i = 1,2,...,n. Maka bentuk hubungan yi dan xi dapat dituliskan sebagai berikut:
yi = a + bixi +ei
Persamaan regresi dari data diatas adalah:
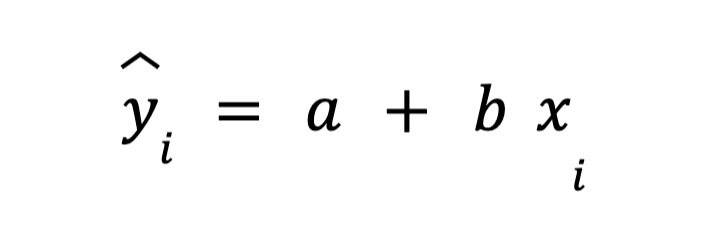
Persamaan error dari kedua persamaan diatas menjadi
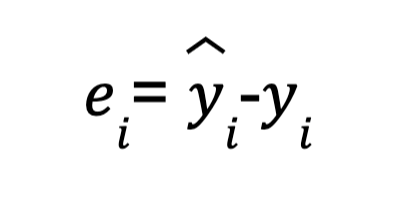
Prinsip dari metode least square adalah metode yang meminimumkan jumlah kuadrat dari error (sum square error atau SSE), sehingga SSE akan bernilai:
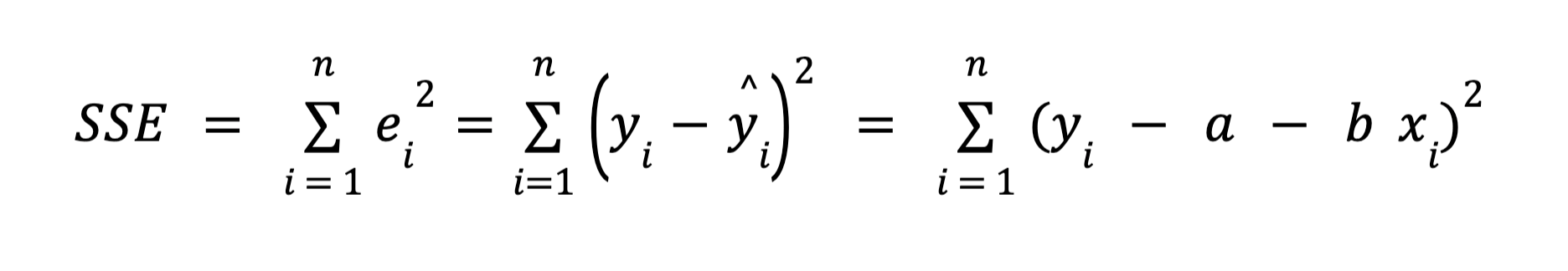
Untuk mendapatkan nilai minimum dari SSE, kita dapat menggunakan prinsip turunan pertama. SSE merupakan fungsi kuadratik yang akan bernilai minimum jika dan hanya jika turunan pertamanya bernilai 0.
Turunan persamaan tersebut terhadap variabel a adalah sebagai berikut:
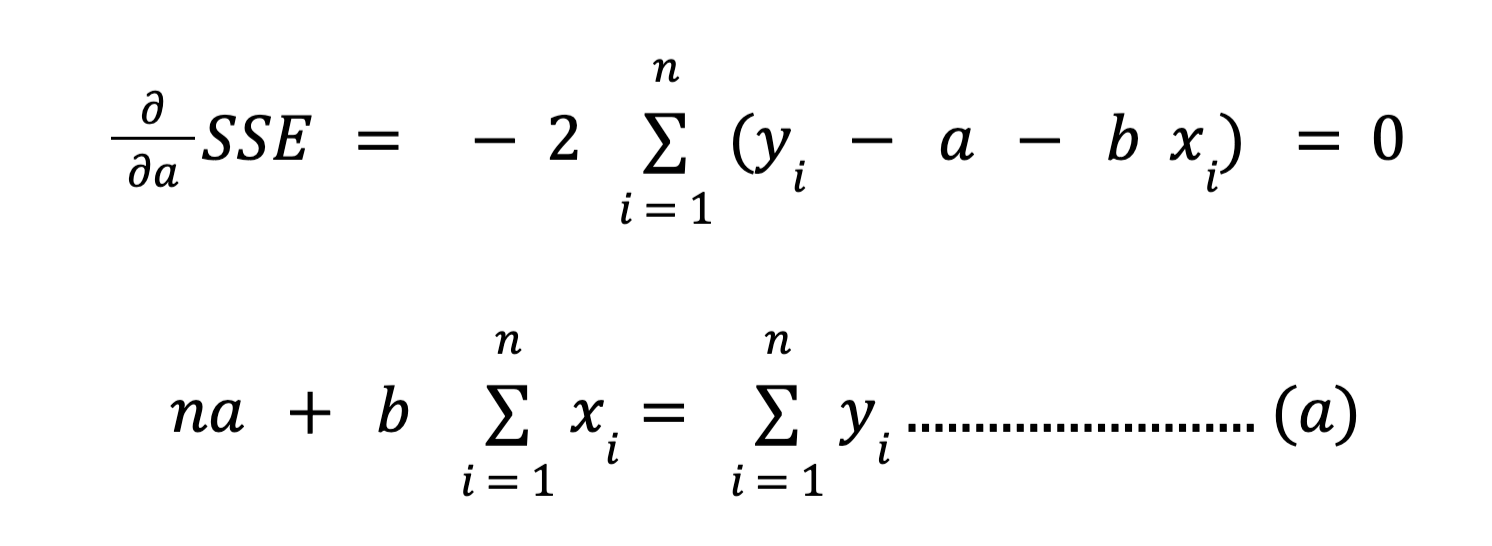
Turunan persamaan tersebut terhadap variabel b adalah sebagai berikut:
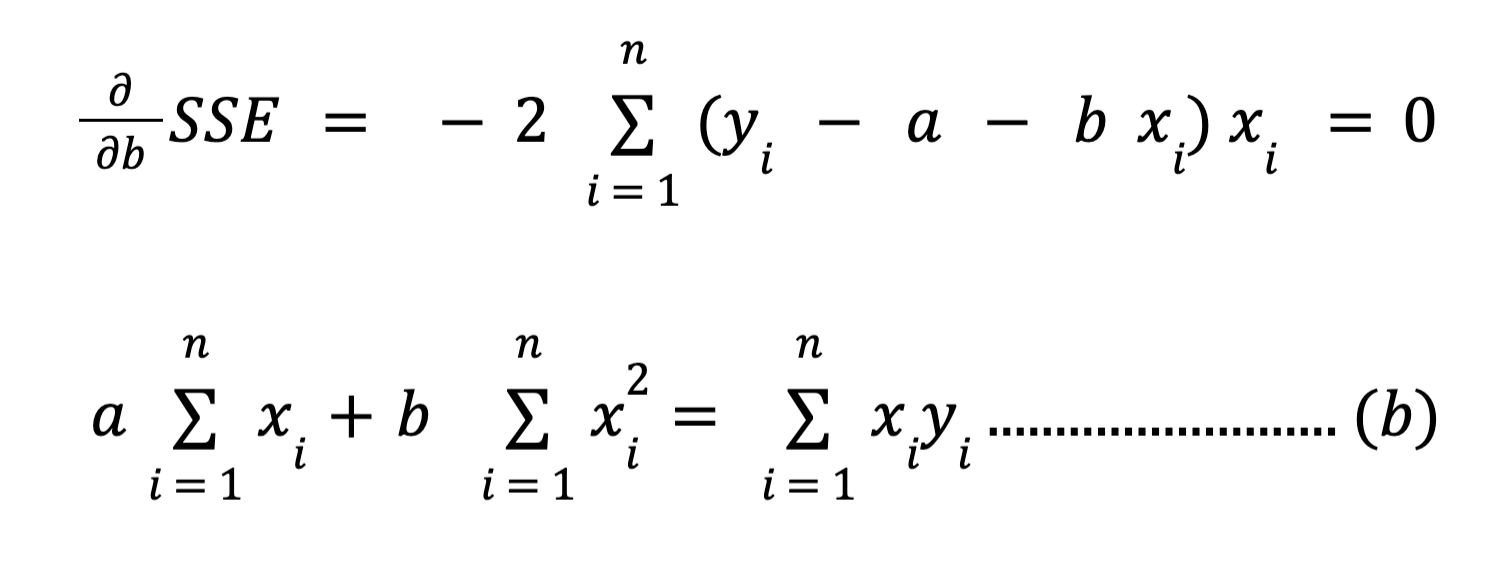
Dengan mensubstitusikan (a) dengan (b), maka diperoleh persamaan untuk variabel a dan b sebagai berikut:
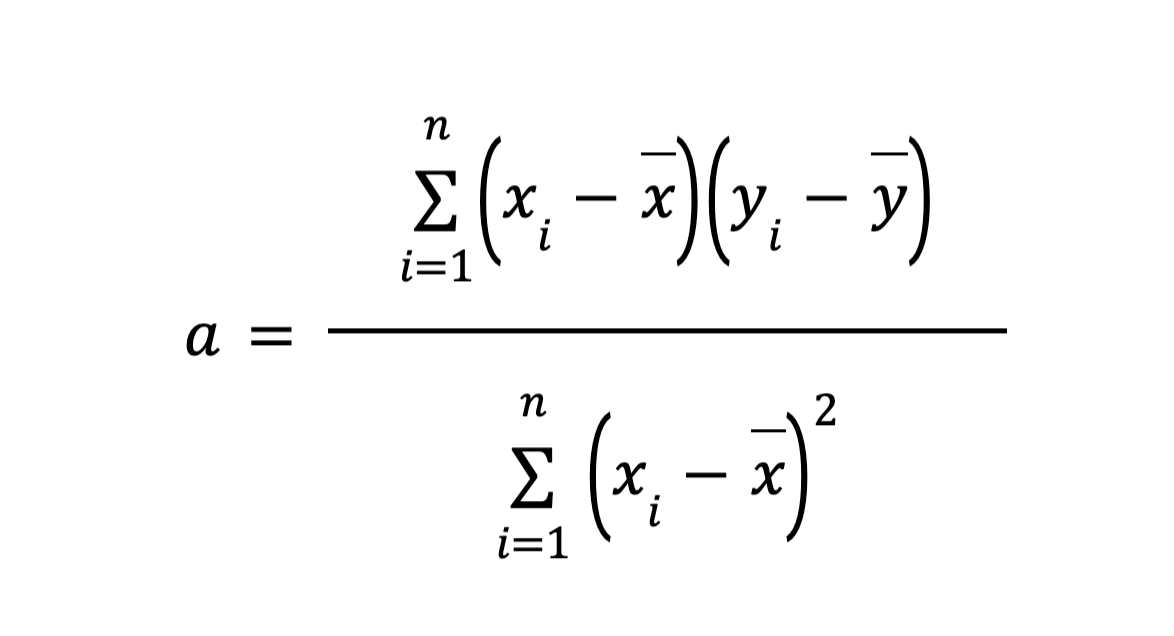
dan
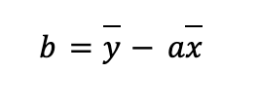
Dimana 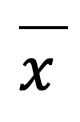 dan
dan 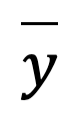 merupakan rata-rata dari variabel X dan Y.
merupakan rata-rata dari variabel X dan Y.
3. Contoh Aplikasi Regresi Linear
Berikut adalah perhitungan koefisien regresi dengan menggunakan metode least square error:
Misalkan kita memiliki data berikut ini. Kita memiliki variabel dependen x dan variabel independen y. Kita memiliki 20 data point dimana kita akan mencoba mencari model regresi linear dari data ini. Pertama-tama kita akan memvisualisasikan data ini kedalam scatterplot untuk dapat mengetahui persebaran datanya.
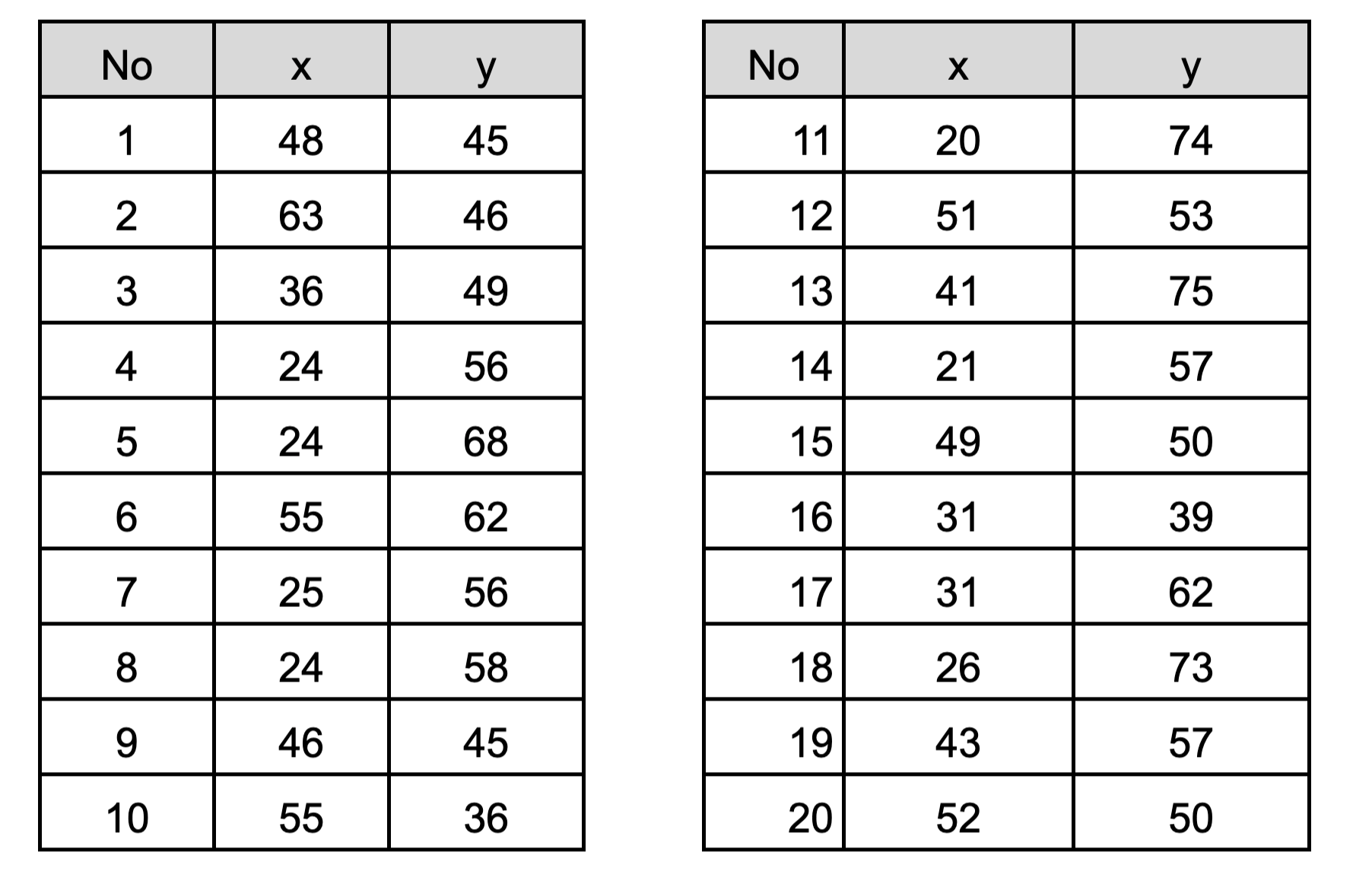
Berikut adalah persebaran data menggunakan scatterplot:
Grafik diatas menunjukkan hubungan variabel X dan variabel Y dimana terlihat bahwa kedua variabel tersebut berkorelasi negatif. Yang berarti semakin tinggi nilai X, maka nilai Y akan semakin kecil.
Dengan menggunakan persamaan diatas, kita akan mencoba mencari model regresi dari dataset yang kita miliki. Variabel x memiliki nilai rata-rata (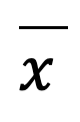 )sebesar 38.25 dan variabel y memiliki rata-rata (
)sebesar 38.25 dan variabel y memiliki rata-rata (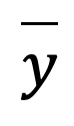 ) sebesar 55.55. Berikut ini adalah perhitungan yang kita butuhkan untuk menghitung nilai koefisien regresi.
) sebesar 55.55. Berikut ini adalah perhitungan yang kita butuhkan untuk menghitung nilai koefisien regresi.
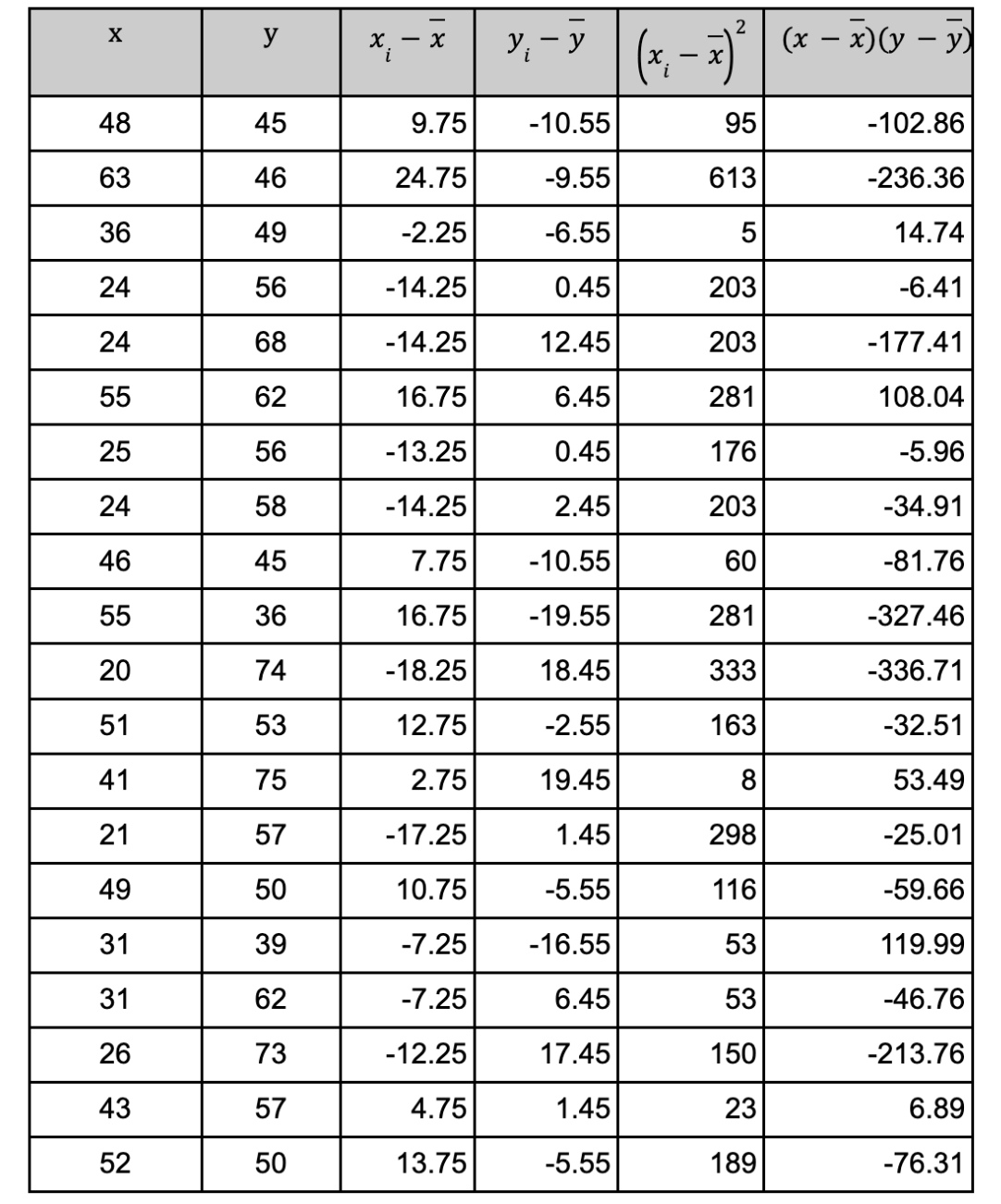
Dengan menggunakan persamaan diatas, kita dapat menentukan nilai a dan b sebagai berikut:
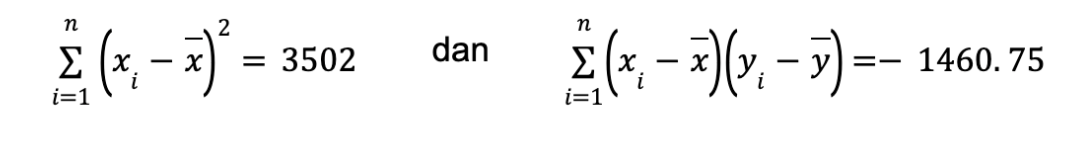
Dengan demikian, kita dapat menentukan kedua koefisien regresi linier ini yaitu
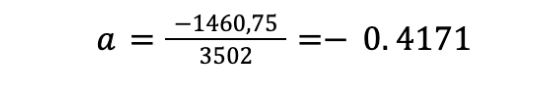
dan

Dengan menggunakan variabel diatas, kita mendapatkan persamaan sebagai berikut:
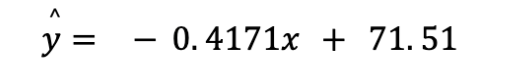
Cukup jelas bukan? Cara diatas adalah metode yang cukup sering digunakan dalam model regresi. Perhitungan diatas cukup banyak melibatkan perhitungan matematis. Namun, teman-teman tidak perlu khawatir. Kita dapat menggunakan bahasa pemrograman R untuk menghitung model regresi dengan cepat.
4. Case Study Regresi Linear
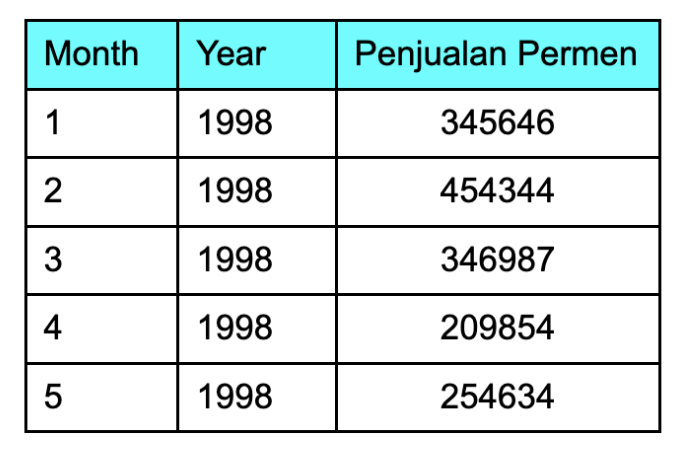
Misalkan kita memiliki data penjualan permen pada bulan Januari, Februari, Maret, April, dan Mei 1998 sebagai berikut:
Kita dapat menggunakan perintah berikut untuk memprediksi kunjungan dokter:
data_prediksi = data.frame( |
Dengan menggunakan metode predict diatas, berikut ini adalah hasil prediksi kunjungan dokter pada bulan Jan-Mei 1998.
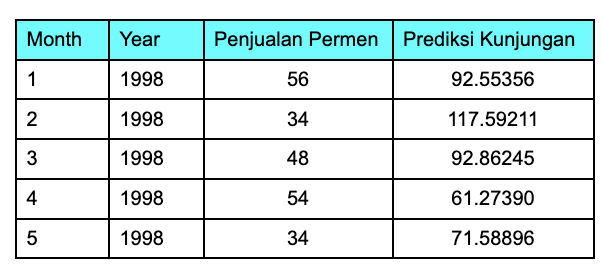
Cukup mudah bukan? Kamu dapat melakukan analisis model regresi dengan cukup mudah menggunakan R.
5. Intepretasi Model Regresi Linear
Berdasarkan model regresi diatas, kita mengetahui bahwa hubungan antara penjualan permen dengan kunjungan ke dokter bersifat positif. Yang berarti bahwa ketika penjualan permen semakin meningkat, maka kunjungan ke dokter akan meningkat juga. Namun efek peningkatan kunjungan dokter ini akan terjadi dalam 4 bulan kedepan.
Model regresi yang dihasilkan dari data diatas yaitu 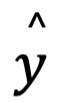 = 12.934 + 0.00023.x . Mari kita mensubstitusikan nilai x dengan 100000, maka nilai kunjungan dokter atau y akan menjadi:
= 12.934 + 0.00023.x . Mari kita mensubstitusikan nilai x dengan 100000, maka nilai kunjungan dokter atau y akan menjadi:
Kunjungan dokter= 12.934 + 0.00023*100000
Kunjungan dokter= 12.934 + 23
Kunjungan dokter= 35.934
Yang dapat berarti, setiap ada kenaikan penjualan permen sebesar 100,000 maka akan meningkatkan kunjungan dokter sebesar 35.934 unit dalam 4 bulan kedepan.
Baca Juga: Belajar Data Science: Bahasa Pemrograman R Cocok untuk Pemula
Simak video dibawah ini yuk untuk lebih jelasnya!
Ingin menjadi seorang praktisi data yang keren dan jago bahasa pemrograman R? Pinter coding nggak harus pinter bahasa pemrograman R aja loh. Paling tidak kamu perlu kuasai bahasa pemrograman yang lainnya juga. Jangan khawatir, semuanya bisa kamu pelajari bersama DQLab!
Untuk menjawab kebutuhan kamu, saat ini DQLab memiliki Modul baru yang fresh dan tentunya real case industry. Agar lebih paham bahasa R, kamu dapat mengakses œR Language, Data Preparation & Exploratory Data Analysis (EDA) - Mengenal Model Regresi Linear & R".
Cara ngerjainnya gimana sih? Gampang banget! Kamu langsung bikin akun DQLab kamu disini. Terus kamu juga bisa akses lebih lengkap modulnya melalui DQLab.id ya. Yuk tunggu apalagi? Ayo persiapkan dirimu untuk berkarir sebagai praktisi data yang kompeten! Selamat mencoba!
Penulis: Reyvan Maulid
Postingan Terkait
Memahami Bahasa R untuk Dunia Professional Part 3
Mulai Karier
sebagai Praktisi
Data Bersama
DQLab
Daftar sekarang dan ambil langkah
pertamamu untuk mengenal
Data Science.


Daftar Gratis & Mulai Belajar
Mulai perjalanan karier datamu bersama DQLab
Sudah punya akun? Kamu bisa Sign in disini
